MD5 Hash

In cryptography, MD5 (Message-Digest algorithm 5) is a widely used cryptographic hash function with a 128-bit hash value. As an Internet standard (RFC 1321), MD5 has been employed in a wide variety of security applications, and is also commonly used to check the integrity of files. An MD5 hash is typically expressed as a 32 digit hexadecimal number.

MD5 is a strengthened version of MD4. Like MD4, the MD5 hash was invented by Professor Ronald Rivest of MIT. Also, MD5 was obviously used as the model for SHA-1, since they share many common features. MD5 and SHA-1 are the two most widely used hash algorithms today, but use of MD5 will certainly decline over time, since it is now considered broken [2,3,4].

The MD5 hash should not be used for cryptographic purposes. To generate the hash of a piece of text, type below:

Input
Calculate
Result

The Algorithm §

The MD5 hash is described in RFC 1321 along with a C implementation. MD5 is similar to the MD4 hash. The padding and initialisation is identical.

MD5 operates on 32-bit words. Let M be the message to be hashed. The message M is padded so that its length (in bits) is equal to 448 modulo 512, that is, the padded message is 64 bits less than a multiple of 512. The padding consists of a single 1 bit, followed by enough zeros to pad the message to the required length. Padding is always used, even if the length of M happens to equal 448 mod 512. As a result, there is at least one bit of padding, and at most 512 bits of padding. Then the length (in bits) of the message (before padding) is appended as a 64-bit block.

The padded message is a multiple of 512 bits and, therefore, it is also a multiple of 32 bits. Let M be the message and N the number of 32-bit words in the (padded) message. Due to the padding, N is a multiple of 16.

A four-word buffer (A,B,C,D) is used to compute the message digest. Here each of A, B, C, D is a 32-bit register. These registers are initialized to the following values in hexadecimal:

word A: 01 23 45 67
word B: 89 ab cd ef
word C: fe dc ba 98
word D: 76 54 32 10

We first define four auxiliary functions that each take as input three 32-bit words and produce as output one 32-bit word.

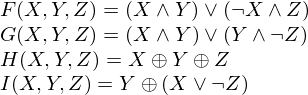
where is logical and, is logical or and is logical xor. Do the following:

/* Process each 16-word block. */
For i = 0 to N/16-1 do

    /* Copy block i into X. */
    For j = 0 to 15 do
        Set X[j] to M[i*16+j].
    end /* of loop on j */

    /* Save A as AA, B as BB, C as CC, and D as DD. */
    AA = A
    BB = B
    CC = C
    DD = D

    /* Round 1. */
    /* Let [abcd k s i] denote the operation
        a = b + ((a + F(b,c,d) + X[k] + T[i]) <<< s). */
    /* Do the following 16 operations. */
    [ABCD  0  7  1]  [DABC  1 12  2]  [CDAB  2 17  3]  [BCDA  3 22  4]
    [ABCD  4  7  5]  [DABC  5 12  6]  [CDAB  6 17  7]  [BCDA  7 22  8]
    [ABCD  8  7  9]  [DABC  9 12 10]  [CDAB 10 17 11]  [BCDA 11 22 12]
    [ABCD 12  7 13]  [DABC 13 12 14]  [CDAB 14 17 15]  [BCDA 15 22 16]

    /* Round 2. */
    /* Let [abcd k s i] denote the operation
        a = b + ((a + G(b,c,d) + X[k] + T[i]) <<< s). */
    /* Do the following 16 operations. */
    [ABCD  1  5 17]  [DABC  6  9 18]  [CDAB 11 14 19]  [BCDA  0 20 20]
    [ABCD  5  5 21]  [DABC 10  9 22]  [CDAB 15 14 23]  [BCDA  4 20 24]
    [ABCD  9  5 25]  [DABC 14  9 26]  [CDAB  3 14 27]  [BCDA  8 20 28]
    [ABCD 13  5 29]  [DABC  2  9 30]  [CDAB  7 14 31]  [BCDA 12 20 32]

    /* Round 3. */
    /* Let [abcd k s t] denote the operation
        a = b + ((a + H(b,c,d) + X[k] + T[i]) <<< s). */
    /* Do the following 16 operations. */
    [ABCD  5  4 33]  [DABC  8 11 34]  [CDAB 11 16 35]  [BCDA 14 23 36]
    [ABCD  1  4 37]  [DABC  4 11 38]  [CDAB  7 16 39]  [BCDA 10 23 40]
    [ABCD 13  4 41]  [DABC  0 11 42]  [CDAB  3 16 43]  [BCDA  6 23 44]
    [ABCD  9  4 45]  [DABC 12 11 46]  [CDAB 15 16 47]  [BCDA  2 23 48]

    /* Round 4. */
    /* Let [abcd k s t] denote the operation
        a = b + ((a + I(b,c,d) + X[k] + T[i]) <<< s). */
    /* Do the following 16 operations. */
    [ABCD  0  6 49]  [DABC  7 10 50]  [CDAB 14 15 51]  [BCDA  5 21 52]
    [ABCD 12  6 53]  [DABC  3 10 54]  [CDAB 10 15 55]  [BCDA  1 21 56]
    [ABCD  8  6 57]  [DABC 15 10 58]  [CDAB  6 15 59]  [BCDA 13 21 60]
    [ABCD  4  6 61]  [DABC 11 10 62]  [CDAB  2 15 63]  [BCDA  9 21 64]

    /* Then perform the following additions. (That is increment each
        of the four registers by the value it had before this block
        was started.) */
    A = A + AA
    B = B + BB
    C = C + CC
    D = D + DD

end /* of loop on i */

The algorithm above uses a set o 64 constants T[i] for i = 1 to 64. Let T[i] denote the i-th element of the table, which is equal to the integer part of 4294967296 times abs(sin(i)), where i is in radians. The elements of the table are given in the appendix of RFC 1321.

Differences between MD5 and MD4 §

The significant differences between MD4 and MD5 are the following:

1. MD5 has four rounds, whereas MD4 has only three. Consequently, the MD5 compression function includes 64 steps, whereas the MD4 compression function has 48 steps.
2. Each step of MD5 has a unique additive constant, T[i], whereas each round of MD4 uses a fixed constant
3. The function G in the second round of MD5 is less symmetric than the G function in MD4
4. Each step of MD5 adds the result of the previous step, which is not the case with MD4. The stated purpose of this modification is to produce a faster avalanche effect.
5. In MD5, the order in which input words are accessed in the second and third rounds is less similar to each other than is the case in MD4.
6. RFC 1321 claims that "the shift amounts in each round have been approximately optimized, to yield a faster ‘avalanche effect’." Also, the shifts employed in each round of MD5 are distinct, which is not the case in MD4.

References §

[1] R. Rivest, RFC 1321 - the MD5 message-digest algorithm, April 1992, at ftp.rfc-editor.org/in-notes/rfc332l.txt

[2] X. Wang and H. Yu, How to break MD5 and other hash functions, at http://www.infosec.sdu.edu.cn/paper/md5-attack.pdf

[3] P. Hawkes, M. Paddon, arid G. G. Rose, Musings on the Wang et al. MD5 collision, at http://eprint.iacr.org/2004/264.pdf

[4] M. Daum, Cryptanalysis of hash functions of the MD4-family, Dissertation zur Erlangurig des Grades eines Doktor der Naturwissenschaften der Ruhr-Universit at Bochum am Fachbereich Mathematik, at www.cits.ruhr-uni-bochum.de/imperia/md/content/magnus/dissmd4.pdf

comments powered by Disqus