Hill Cipher

Introduction §

Invented by Lester S. Hill in 1929, the Hill cipher is a polygraphic substitution cipher based on linear algebra. Hill used matrices and matrix multiplication to mix up the plaintext.

To counter charges that his system was too complicated for day to day use, Hill constructed a cipher machine for his system using a series of geared wheels and chains. However, the machine never really sold.

Hill's major contribution was the use of mathematics to design and analyse cryptosystems. It is important to note that the analysis of this algorithm requires a branch of mathematics known as number theory. Many elementary number theory text books deal with the theory behind the Hill cipher, with several talking about the cipher in detail (e.g. Elementary Number Theory and its applications, Rosen, 2000). It is advisable to get access to a book such as this, and to try to learn a bit if you want to understand this algorithm in depth.

For a guide on how to break Hill ciphers, see Cryptanalysis of the Hill Cipher.

Example §

This example will rely on some linear algebra and some number theory. The key for a hill cipher is a matrix e.g.

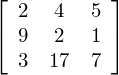
In the above case, we have taken the size to be 3×3, however it can be any size (as long as it is square). Assume we want to encipher the message ATTACK AT DAWN. To encipher this, we need to break the message into chunks of 3. We now take the first 3 characters from our plaintext, ATT and create a vector that corresponds to the letters (replace A with 0, B with 1 ... Z with 25 etc.) to get: [0 19 19] (this is ['A' 'T' 'T']).

To get our ciphertext we perform a matrix multiplication (you may need to revise matrix multiplication if this doesn't make sense):

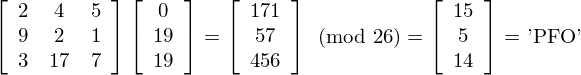
This process is performed for all 3 letter blocks in the plaintext. The plaintext may have to be padded with some extra letters to make sure that there is a whole number of blocks.

Now for the tricky part, the decryption. We need to find an inverse matrix modulo 26 to use as our 'decryption key'. i.e. we want something that will take 'PFO' back to 'ATT'. If our 3 by 3 key matrix is called K, our decryption key will be the 3 by 3 matrix K^-1, which is the inverse of K.

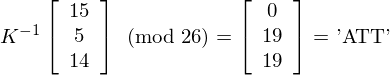
To find K^-1 we have to use a bit of maths. It turns out that K^-1 above can be calculated from our key. A lengthy discussion will not be included here, but we will give a short example. The important things to know are inverses (mod m), determinants of matrices, and matrix adjugates.

Let K be the key matrix. Let d be the determinant of K. We wish to find K^-1 (the inverse of K), such that K × K^-1 = I (mod 26), where I is the identity matrix. The following formula tells us how to find K^-1 given K:

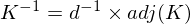
where d × d^-1 = 1(mod 26), and adj(K) is the adjugate matrix of K.

d (the determinant) is calculated normally for K (for the example above, it is 489 = 21 (mod 26)). The inverse, d^-1, is found by finding a number such that d × d^-1 = 1 (mod 26) (this is 5 for the example above since 5*21 = 105 = 1 (mod 26)). The simplest way of doing this is to loop through the numbers 1..25 and find the one such that the equation is satisfied. There is no solution (i.e. choose a different key) if gcd(d,26) ≠ 1 (this means d and 26 share factors, if this is the case K can not be inverted, this means the key you have chosen will not work, so choose another one).

That is it. Once K^-1 is found, decryption can be performed.

JavaScript Example of the Hill Cipher §

This is a JavaScript implementation of the Hill Cipher. The case here is restricted to 2x2 case of the hill cipher for now, it may be expanded to 3x3 later.

The 'key' should be input as 4 numbers, e.g. 3 4 19 11. These numbers will form the key (top row, bottom row).

Plaintext
the gold is buried in orono

key =

Ciphertext

Cryptanalysis §

Cryptanalysis is the art of breaking codes and ciphers. When attempting to crack a Hill cipher, frequency analysis will be practically useless, especially as the size of the key block increases. For very long ciphertexts, frequency analysis may be useful when applied to bigrams (for a 2 by 2 hill cipher), but for short ciphertexts this will not be practical.

For a guide on how to break Hill ciphers with a crib, see Cryptanalysis of the Hill Cipher.

The basic Hill cipher is vulnerable to a known-plaintext attack, however,(if you know the plaintext and corresponding ciphertext the key can be recovered) because it is completely linear. An opponent who intercepts several plaintext/ciphertext character pairs can set up a linear system which can (usually) be easily solved; if it happens that this system is indeterminate, it is only necessary to add a few more plaintext/ciphertext pairs[1]. The known ciphertext attack is the best one to try when trying to break the hill cipher, if no sections of the plaintext are known, guesses can be made.

For the case of a 2 by 2 hill cipher, we could attack it by measuring the frequencies of all the digraphs that occur in the ciphertext. In standard english, the most common digraph is 'th', followed by 'he'. If we know the hill cipher has been employed and the most common digraph is 'kx', followed by 'vz' (for example), we would guess that 'kx' and 'vz' correspond to 'th' and 'he', respectively. This would mean [19, 7] and [7, 4] are sent to [10, 23] and [21, 25] respectively (after substituting letters for numbers). If K was the encrypting matrix, we would have:

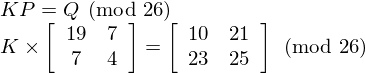
Since the inverse of P is

we have

which gives us a possible key. After attempting to decrypt the ciphertext with

we would know whether our guess was correct. If it is not, we could try other combinations of common ciphertext digraphs until we get something that is correct.

In general, the hill cipher will not be used on its own, since it is not all that secure. It is, however, still a useful step when combined with other non-linear operations, such as S-boxes (in modern ciphers). It is generally used because matrix multiplication provides good diffusion (it mixes things up nicely). Some modern ciphers use a matrix multiplication step to provide diffusion e.g. AES and Twofish use matrix multiplication as a part of their algorithms.

References §

• [1] Wikipedia has a good description of the encryption/decryption process, history and cryptanalysis of this algorithm
• Rosen, K (2000). Elementary Number Theory and its applications. Addison Wesley Longman, ISBN 0-321-20442-5.M.

comments powered by Disqus