Gaussian Mixture Model Tutorial
A Gaussian Mixture Model (GMM) is a probability distribution. Where basic distributions like the Gaussian or Cauchy distributions model a single peak, GMMs can model distributions with many peaks. This is achieved by adding several Gaussiand together. By using a sufficient number of Gaussians, and by adjusting their means and covariances as well as the weights, almost any continuous density can be approximated to arbitrary accuracy. A mixture of Gaussians can be written as:
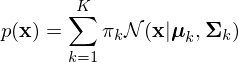
where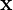 
is a 
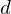dimensional vector, 
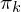is the weight of the 
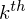gaussian component, 
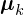is the
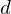dimensional vector of means for the 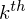gaussian component and 
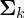is the 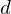by 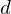covariance matrix for the 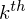gaussian component. 
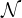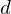is a dimensional gaussian of the form:
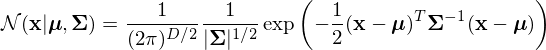
where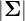 
is the determinant of 
.
GMMs are commonly used to model speaker characteristics in automatic speaker recognition systems.
The Expectation Maximisation Algorithm §
Finding the optimal gaussian mixture parameters for given a set of observations is performed using the Expectation Maximisation (EM) algorithm.
The EM algorithm is a maximum likelyhood approach similar in structure to the k-means algorithm. It is an iterative algorithm with 2 steps per
iteration: the expectation (E) step and the maximisation (M) step. The update of the gaussian mixture parameters from an E step followed by
an M step is guaranteed to increase the log likelyhood function (the likelyhood that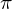 
, 
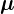and are the mixture parameters
that generated the given set of observations).
The steps involved in the EM algorithm are listed below.
- Initialise the means 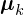, covariances 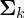and mixing coefficients 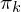, and the initial value of the log likelyhood. The k-means algorithm is commonly used to cluster the given observations, these clusters are then provided as the starting point for the EM algorithm.
- E step Evaluate the responsibilities using the current parameter values
- M step Re-estimate the parameters using the current responsibilities
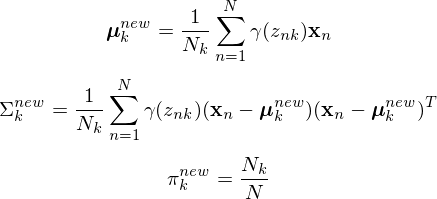
where
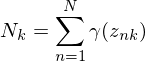
- Evaluate the log likelyhood
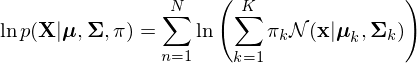
Check for convergence of either the parameters or the log likelyhood. If the convergence criterion is not satisfied, return to step 2.