Encoding Variables For Neural Networks

Deep Neural Networks have become more popular over the last few years, this page will deal with methods for encoding target variables. The headings are the type of target, real numbers are for standard regression problems. Categorical targets are for things that like predicting whether something is red, blue or green. There are also situations where you want to predict angles, these are different to real numbers because 360 is equal to 0, but if you treat them as real numbers the classifier won't know that.

Real Numbers §

There is not much to say about real numbers, neural networks naturally output real numbers so no modifications are necessary.

Categorical Variables §

Categorical variables should be split into what is known as 1-hot encoding or 1-of-k encoding. If your labels are e.g. red, green and blue, you would create a set of three outputs for the neural network, red = [1,0,0], green = [0,1,0] and blue = [0,0,1]. When performing predictions, put an input through the network then choose as the label whichever output is highest. For example if the output were [0.2, 0.3, 0.5], we would predict blue.

Some problems have thousands of output labels, and you simply have to create thousands of 1-hot output variables for each class. You will generally need quite a lot of training information to get reliable predictions for so many classes though.

Angles §

When predicting angles you generally want a number between 0 and 360 degrees, along with the fact that 360==0. If you treat the angles as standard real numbers with a squared error loss function the neural net will assume that 360 and 0 degrees are actually very far apart, this means the predictions near these extremes will not be very good. 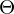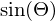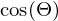To avoid this it is better to create two variables, instead of predicting just the angle , it is better to predict and separately. This has the added advantage of being normalised between -1 and 1.

When doing the prediction, this means you will get two numbers output instead of just 1 angle. To reconstruct the angle, assume the neural net outputs 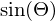and 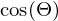, then:

You will generally get much better performance when predicting angles in this manner than predicting the angles directly. This is true for predicting any real numbers modulo another number, just map the numbers to angles, then use sin and cos. This prevents any issues around the limits.

comments powered by Disqus