MD5 Hash
In cryptography, MD5 (Message-Digest algorithm 5) is a widely used cryptographic hash function with a 128-bit hash value. As an Internet standard (RFC 1321), MD5 has been employed in a wide variety of security applications, and is also commonly used to check the integrity of files. An MD5 hash is typically expressed as a 32 digit hexadecimal number.
MD5 is a strengthened version of MD4. Like MD4, the MD5 hash was invented by Professor Ronald Rivest of MIT. Also, MD5 was obviously used as the model for SHA-1, since they share many common features. MD5 and SHA-1 are the two most widely used hash algorithms today, but use of MD5 will certainly decline over time, since it is now considered broken [2,3,4].
The MD5 hash should not be used for cryptographic purposes. To generate the hash of a piece of text, type below:
The Algorithm §
The MD5 hash is described in RFC 1321 along with a C implementation. MD5 is similar to the MD4 hash. The padding and initialisation is identical.
MD5 operates on 32-bit words. Let M be the message to be hashed. The message M is padded so that its length (in bits) is equal to 448 modulo 512, that is, the padded message is 64 bits less than a multiple of 512. The padding consists of a single 1 bit, followed by enough zeros to pad the message to the required length. Padding is always used, even if the length of M happens to equal 448 mod 512. As a result, there is at least one bit of padding, and at most 512 bits of padding. Then the length (in bits) of the message (before padding) is appended as a 64-bit block.
The padded message is a multiple of 512 bits and, therefore, it is also a multiple of 32 bits. Let M be the message and N the number of 32-bit words in the (padded) message. Due to the padding, N is a multiple of 16.
A four-word buffer (A,B,C,D) is used to compute the message digest. Here each of A, B, C, D is a 32-bit register. These registers are initialized to the following values in hexadecimal:
word A: 01 23 45 67 word B: 89 ab cd ef word C: fe dc ba 98 word D: 76 54 32 10
We first define four auxiliary functions that each take as input three 32-bit words and produce as output one 32-bit word.
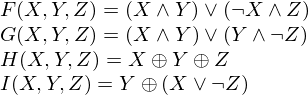
where  is logical and,
is logical and,  is logical or and
is logical or and
 is logical xor. Do the following:
is logical xor. Do the following:
/* Process each 16-word block. */ For i = 0 to N/16-1 do /* Copy block i into X. */ For j = 0 to 15 do Set X[j] to M[i*16+j]. end /* of loop on j */ /* Save A as AA, B as BB, C as CC, and D as DD. */ AA = A BB = B CC = C DD = D /* Round 1. */ /* Let [abcd k s i] denote the operation a = b + ((a + F(b,c,d) + X[k] + T[i]) <<< s). */ /* Do the following 16 operations. */ [ABCD 0 7 1] [DABC 1 12 2] [CDAB 2 17 3] [BCDA 3 22 4] [ABCD 4 7 5] [DABC 5 12 6] [CDAB 6 17 7] [BCDA 7 22 8] [ABCD 8 7 9] [DABC 9 12 10] [CDAB 10 17 11] [BCDA 11 22 12] [ABCD 12 7 13] [DABC 13 12 14] [CDAB 14 17 15] [BCDA 15 22 16] /* Round 2. */ /* Let [abcd k s i] denote the operation a = b + ((a + G(b,c,d) + X[k] + T[i]) <<< s). */ /* Do the following 16 operations. */ [ABCD 1 5 17] [DABC 6 9 18] [CDAB 11 14 19] [BCDA 0 20 20] [ABCD 5 5 21] [DABC 10 9 22] [CDAB 15 14 23] [BCDA 4 20 24] [ABCD 9 5 25] [DABC 14 9 26] [CDAB 3 14 27] [BCDA 8 20 28] [ABCD 13 5 29] [DABC 2 9 30] [CDAB 7 14 31] [BCDA 12 20 32] /* Round 3. */ /* Let [abcd k s t] denote the operation a = b + ((a + H(b,c,d) + X[k] + T[i]) <<< s). */ /* Do the following 16 operations. */ [ABCD 5 4 33] [DABC 8 11 34] [CDAB 11 16 35] [BCDA 14 23 36] [ABCD 1 4 37] [DABC 4 11 38] [CDAB 7 16 39] [BCDA 10 23 40] [ABCD 13 4 41] [DABC 0 11 42] [CDAB 3 16 43] [BCDA 6 23 44] [ABCD 9 4 45] [DABC 12 11 46] [CDAB 15 16 47] [BCDA 2 23 48] /* Round 4. */ /* Let [abcd k s t] denote the operation a = b + ((a + I(b,c,d) + X[k] + T[i]) <<< s). */ /* Do the following 16 operations. */ [ABCD 0 6 49] [DABC 7 10 50] [CDAB 14 15 51] [BCDA 5 21 52] [ABCD 12 6 53] [DABC 3 10 54] [CDAB 10 15 55] [BCDA 1 21 56] [ABCD 8 6 57] [DABC 15 10 58] [CDAB 6 15 59] [BCDA 13 21 60] [ABCD 4 6 61] [DABC 11 10 62] [CDAB 2 15 63] [BCDA 9 21 64] /* Then perform the following additions. (That is increment each of the four registers by the value it had before this block was started.) */ A = A + AA B = B + BB C = C + CC D = D + DD end /* of loop on i */
The algorithm above uses a set o 64 constants T[i] for i = 1 to 64. Let T[i] denote the i-th element of the table, which is equal to the integer part of 4294967296 times abs(sin(i)), where i is in radians. The elements of the table are given in the appendix of RFC 1321.
Differences between MD5 and MD4 §
The significant differences between MD4 and MD5 are the following:
- MD5 has four rounds, whereas MD4 has only three. Consequently, the MD5 compression function includes 64 steps, whereas the MD4 compression function has 48 steps.
- Each step of MD5 has a unique additive constant, T[i], whereas each round of MD4 uses a fixed constant
- The function G in the second round of MD5 is less symmetric than the G function in MD4
- Each step of MD5 adds the result of the previous step, which is not the case with MD4. The stated purpose of this modification is to produce a faster avalanche effect.
- In MD5, the order in which input words are accessed in the second and third rounds is less similar to each other than is the case in MD4.
- RFC 1321 claims that "the shift amounts in each round have been approximately optimized, to yield a faster ‘avalanche effect’." Also, the shifts employed in each round of MD5 are distinct, which is not the case in MD4.
References §
[1] R. Rivest, RFC 1321 - the MD5 message-digest algorithm, April 1992, at ftp.rfc-editor.org/in-notes/rfc332l.txt
[2] X. Wang and H. Yu, How to break MD5 and other hash functions, at http://www.infosec.sdu.edu.cn/paper/md5-attack.pdf
[3] P. Hawkes, M. Paddon, arid G. G. Rose, Musings on the Wang et al. MD5 collision, at http://eprint.iacr.org/2004/264.pdf
[4] M. Daum, Cryptanalysis of hash functions of the MD4-family, Dissertation zur Erlangurig des Grades eines Doktor der Naturwissenschaften der Ruhr-Universit at Bochum am Fachbereich Mathematik, at www.cits.ruhr-uni-bochum.de/imperia/md/content/magnus/dissmd4.pdf
comments powered by Disqus