Simple Substitution Cipher

Introduction §

The simple substitution cipher is a cipher that has been in use for many hundreds of years (an excellent history is given in Simon Singhs 'the Code Book'). It basically consists of substituting every plaintext character for a different ciphertext character. It differs from the Caesar cipher in that the cipher alphabet is not simply the alphabet shifted, it is completely jumbled.

The simple substitution cipher offers very little communication security, and it will be shown that it can be easily broken even by hand, especially as the messages become longer (more than several hundred ciphertext characters).

Example §

Here is a quick example of the encryption and decryption steps involved with the simple substitution cipher. The text we will encrypt is 'defend the east wall of the castle'.

Keys for the simple substitution cipher usually consist of 26 letters (compared to the caeser cipher's single number). An example key is:

plain alphabet : abcdefghijklmnopqrstuvwxyz
cipher alphabet: phqgiumeaylnofdxjkrcvstzwb

An example encryption using the above key:

plaintext : defend the east wall of the castle
ciphertext: giuifg cei iprc tpnn du cei qprcni

It is easy to see how each character in the plaintext is replaced with the corresponding letter in the cipher alphabet. Decryption is just as easy, by going from the cipher alphabet back to the plain alphabet. When generating keys it is popular to use a key word, e.g. 'zebra' to generate it, since it is much easier to remember a key word compared to a random jumble of 26 characters. Using the keyword 'zebra', the key would become:

cipher alphabet: zebracdfghijklmnopqstuvwxy

This key is then used identically to the example above. If your key word has repeated characters e.g. 'mammoth', be careful not to include the repeated characters in the cipher alphabet.

JavaScript Example §

Plaintext

key =

Remove Punctuation

Ciphertext

Other Implementations §

To encipher your own messages in python, you can use the pycipher module. To install it, use pip install pycipher. To encipher messages with the substitution cipher (or another cipher, see here for documentation):

>>>from pycipher import SimpleSubstitution
>>>ss = SimpleSubstitution('phqgiumeaylnofdxjkrcvstzwb')
>>>ss.encipher('defend the east wall of the castle')
'GIUIFGCEIIPRCTPNNDUCEIQPRCNI'
>>>ss.decipher('GIUIFGCEIIPRCTPNNDUCEIQPRCNI')
'DEFENDTHEEASTWALLOFTHECASTLE'

Cryptanalysis §

See Cryptanalysis of the Substitution Cipher for a guide on how to automatically break this cipher.

The simple substitution cipher is quite easy to break. Even though the number of keys is around 2^88.4 (a really big number), there is a lot of redundancy and other statistical properties of english text that make it quite easy to determine a reasonably good key. The first step is to calculate the frequency distribution of the letters in the cipher text. This consists of counting how many times each letter appears. Natural english text has a very distinct distribution that can be used help crack codes. This distribution is as follows:

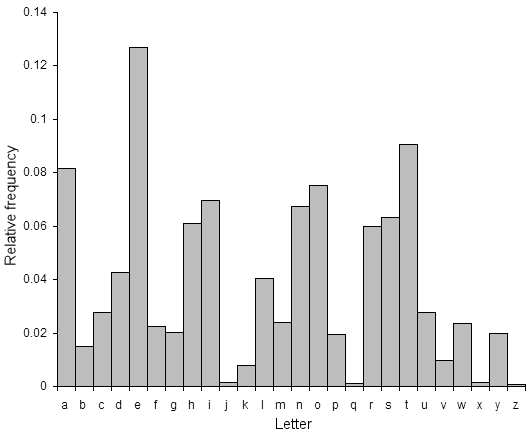
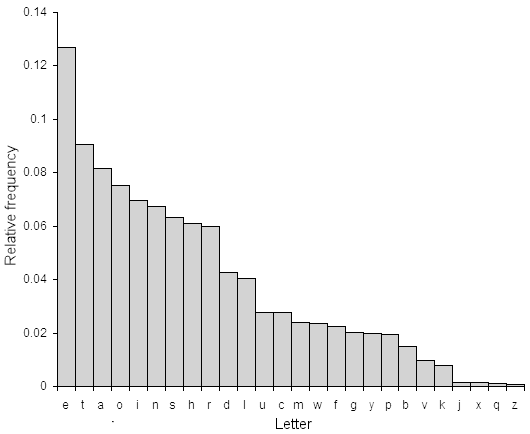
Letter distribution — English Letter Frequencies

This means that the letter 'e' is the most common, and appears almost 13% of the time, whereas 'z' appears far less than 1 percent of time. Application of the simple substitution cipher does not change these letter frequncies, it merely jumbles them up a bit (in the example above, 'e' is enciphered as 'i', which means 'i' will be the most common character in the cipher text). A cryptanalyst has to find the key that was used to encrypt the message, which means finding the mapping for each character. For reasonably large pieces of text (several hundred characters), it is possible to just replace the most common ciphertext character with 'e', the second most common ciphertext character with 't' etc. for each character (replace according to the order in the image on the right). This will result in a very good approximation of the original plaintext, but only for pieces of text with statistical properties close to that for english, which is only guaranteed for long tracts of text.

Short pieces of text often need more expertise to crack. If the original punctuation exists in the message, e.g. 'giuifg cei iprc tpnn du cei qprcni', then it is possible to use the following rules to guess some of the words, then, using this information, some of the letters in the cipher alphabet are known.

One-Letter Words	a, I.
Frequent Two-Letter Words	of, to, in, it, is, be, as, at, so, we, he, by, or, on, do, if, me, my, up, an, go, no, us, am
Frequent Three-Letter Words	the, and, for, are, but, not, you, all, any, can, had, her, was, one, our, out, day, get, has, him, his, how, man, new, now, old, see, two, way, who, boy, did, its, let, put, say, she, too, use
Frequent Four-Letter Words	that, with, have, this, will, your, from, they, know, want, been, good, much, some, time

* the information in the above table was borrowed from Simon Singhs website, http://www.simonsingh.net/The_Black_Chamber/hintsandtips.htm

Usually, punctuation in ciphertext is removed and the ciphertext is put into blocks such as 'giuif gceii prctp nnduc eiqpr cnizz', which prevents the previous tricks from working. There are, however, many other characteristics of english that can be utilized. The table below lists some other facts that can be used to determine the correct key. Only the few most common examples are given for each rule.

For information about other languages, see Letter frequencies for various languages.

Most Frequent Single Letters	E T A O I N S H R D L U
Most Frequent Digraphs	th er on an re he in ed nd ha at en es of or nt ea ti to it st io le is ou ar as de rt ve
Most Frequent Trigraphs	the and tha ent ion tio for nde has nce edt tis oft sth men
Most Common Doubles	ss ee tt ff ll mm oo
Most Frequent Initial Letters	T O A W B C D S F M R H I Y E G L N P U J K
Most Frequent Final Letters	E S T D N R Y F L O G H A K M P U W

* the information in the above table was borrowed from Simon Singhs website, http://www.simonsingh.net/The_Black_Chamber/hintsandtips.htm

There are more tricks that can be used besides the ones listed here, maybe one day they will be included here. In the meantime use your favourite search engine to find more information.

References §

Wikipedia has a good description of the encryption/decryption process, history and cryptanalysis of this algorithm
Simon Singh's 'The Code Book' is an excellent introduction to ciphers and codes, and includes a section on substitution ciphers.
Singh, Simon (2000). The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography. ISBN 0-385-49532-3.

Simon Singh's web site has some good substitution cipher solving tools: